Complete Knapsack Problem
2023-11-27 21:14:38 # Algorithm #DP #Knapsack

完全背包和0-1背包的区别

完全背包和0-1背包的区别在于，完全背包是同一个物品可以选很多次。

在求完全背包情况下刚好装满背包的最大值：
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-k*weights[i]]+k*values[i])

这里就是两种情况，选这个物品k次或者不选这个物品。

Leetcode 322 Coin Change

关于初始化的问题

当问题要求背包被恰好装满时，我们通过将除了dp[i][0]之外的所有值设置为-∞或∞来实现(根据题目是求最大还是最小值)。dp[i][0]设为0，因为当amount为0的时候，是有解的。

当问题只要求物品的总重量不超过背包容量时，我们将dp[∗][∗]的所有值设置为0。

原始解法：三层for循环

我们在写代码的时候，会循环遍历k。我们会从0开始，这样能代表不选到选k次的情况。但注意，需要与上次迭代所得到的答案dp[i][j]进行比较，所以代码要写成：

1
2
3
for(int k = 0;k<= j/coins[i-1];k++){
    dp[i][j] = Math.min(dp[i][j],dp[i-1][j-k*coins[i-1]]+k);
}

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        //dp[i][j]=>注意这里的i是指从前i件物品中进行选择
        int[][] dp = new int[n+1][amount+1];
        
        //因为我们要求恰好装满背包，所以初始状态应该为一个错误的值，比如正无穷或负无穷
        //因为这道题是求最小值，所以我们初始化可以设置为最大值或amount+1(也是不可达的值)
        for(int i = 0; i <= n; i++) {
            Arrays.fill(dp[i], amount + 1);
        }
        //当amount为0时
        for(int i = 0;i<=n;i++){
            dp[i][0]= 0;
        }

        // Start filling the dp table
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= amount; j++) {
                //当前物品选k次
                for(int k = 0;k<= j/coins[i-1];k++){
                    dp[i][j] = Math.min(dp[i][j],dp[i-1][j-k*coins[i-1]]+k);
                }
            }
        }

        return dp[n][amount] > amount ? -1 : dp[n][amount];
    }
}

优化I：两层for循环

需要注意的是，上面所提到的k次是可以被优化掉的。

优化后的式子：dp[i][j] = Math.max(dp[i-1][j], dp[i][j-coins[i]]+values[i])

注意第二个变成了dp[i][j-coins[i]+values[i]，因为我们用dp[i]来代替了之前所有的选过的i的计算（这里用数学方法也能证明，但建议直接理解这个式子）。

因此，我们可以利用已有的dp值来更新dp，而不需要额外的k循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        //dp[i][j]=>注意这里的i是指从前i件物品中进行选择
        int[][] dp = new int[n+1][amount+1];
        
        //因为我们要求恰好装满背包，所以初始状态应该为一个错误的值，比如正无穷或负无穷
        //因为这道题是求最小值，所以我们初始化可以设置为最大值或amount+1(也是不可达的值)
        for(int i = 0; i <= n; i++) {
            Arrays.fill(dp[i], amount + 1);
        }
        //当amount为0时
        for(int i = 0;i<=n;i++){
            dp[i][0]= 0;
        }

        // Start filling the dp table
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= amount; j++) {
                if(j>=coins[i-1]){
                    //容量够，可以选也可以不选
                    dp[i][j] = Math.min(dp[i-1][j],dp[i][j-coins[i-1]]+1);
                }else{
                    //容量不够就不选
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[n][amount] > amount ? -1 : dp[n][amount];
    }
}

优化II：一层for循环

我们发现dp[i][j]是依赖于左方和正上方的值，因此我们要在计算dp[i][j]的时候，保证左方和正上方都已经计算出出来
类似于下面这个图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
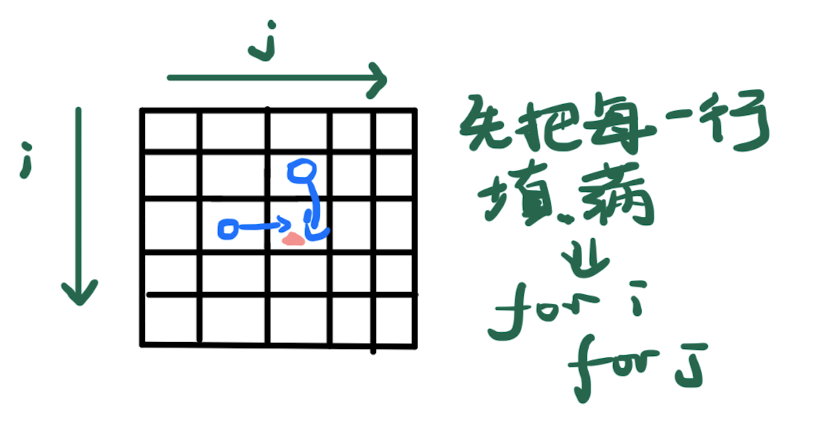
26
class Solution {
    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        //dp[i][j]=>注意这里的i是指从前i件物品中进行选择
        int[] dp = new int[amount+1];
        
        //因为我们要求恰好装满背包，所以初始状态应该为一个错误的值，比如正无穷或负无穷
        //因为这道题是求最小值，所以我们初始化可以设置为最大值或amount+1(也是不可达的值)
        for(int j = 0; j <= amount; j++) {
            dp[j] = amount+1;
        }
        //当amount为0时
        dp[0]= 0;

        // Start filling the dp table
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= amount; j++) {
                if(j>=coins[i-1]){
                    //容量够，可以选也可以不选
                    dp[j] = Math.min(dp[j],dp[j-coins[i-1]]+1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
}
Prev
2023-11-27 21:14:38 # Algorithm #DP #Knapsack
Next