Hash, Mac, and Digital Signature

Hash functions

• One-way security
  • h= H(m), knowing H(m) but should still be hard to find h(input)
• COL: collision-resistance security
  • computationally infeasible to find any pair of distinct messages m1, m2 such that h1=H(m1) is equal to h2=H(m2)
  • Find collision using ≈√(2^n )=2^(n/2) random inputs to H

Message Authentication Code(MAC)

• MAC is fast, and it has similar building blocks as symmetric key encryption.

• is a many-to-one function

  • many messages generate the same MAC

• Both Sender and Reciever can send MAC since they both have the same secret key.

CMAC

CMAC is a CBC mode for authentication, and it will use the final block as a MAC.

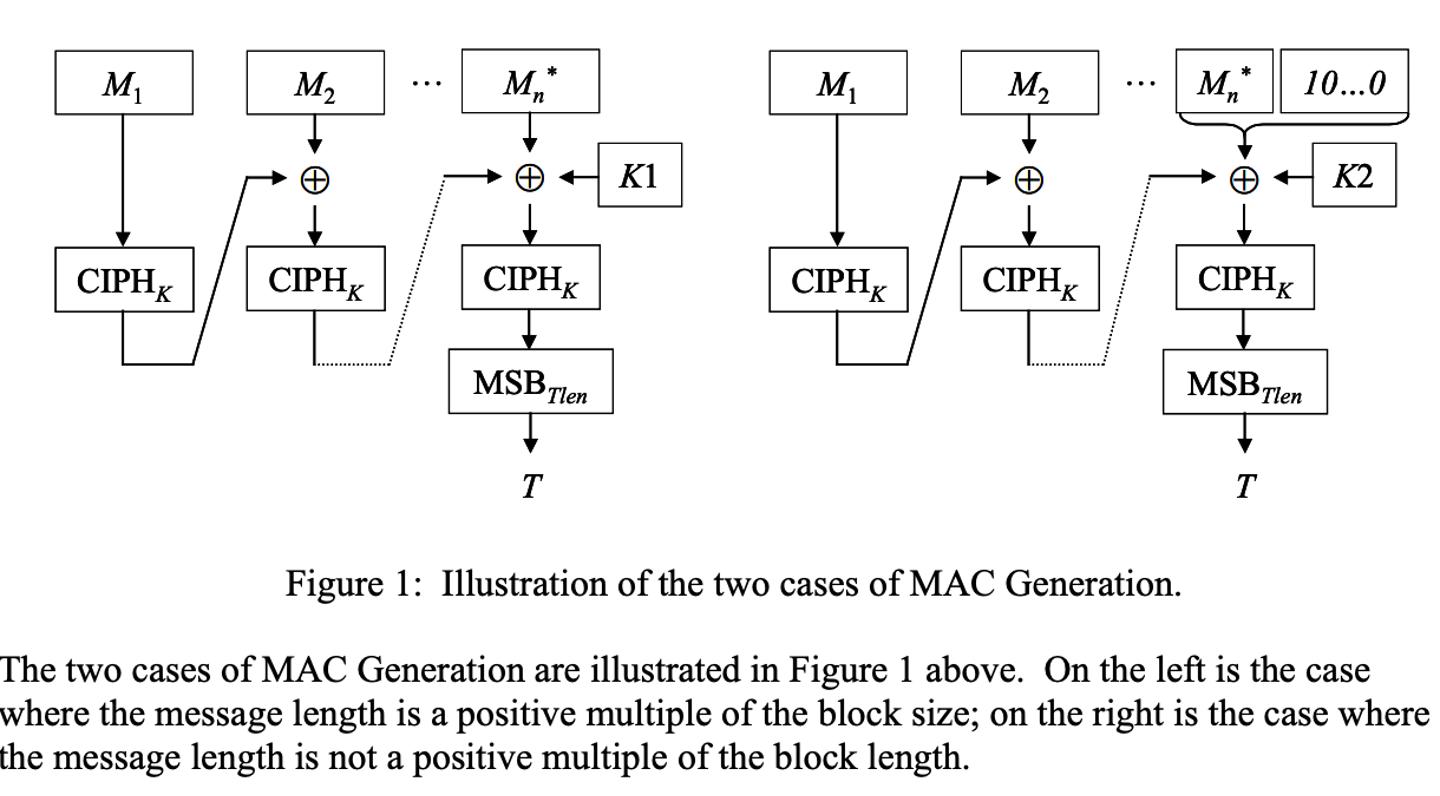
HMAC

A MAC based on a hash function.

HMAC(K,M)= Hash[(K+ XOR opad) || Hash[(K+ XOR ipad) || M)] ]

Digital signatures

The digital signature is slow.

Properties

• Verifies author
  • UNForgebale
  • Undeniable - non-repudiatable
• universally verifiable

Problems - why use it?

There’s a significant risk that Alice cannot authenticate Bob. In other words, another person Peter can pretend to be Bob, and send his public key to Alice, and then Alice will generate a shared key using Peter’s public key. In this case, Peter would decrypt the messages that Alice sends to Bob.

This is the so-called Man in the middle attack.

Thus, cryptographist were trying to find a more secure way.

Digital signature is used for proving authenticity of the origin of documents as well as for non-repudiation as it can prove the authenticity of the signer.

Another use of digital signature is to ensure the integrity of the messages against unauthorized modification

Generate digital signatures


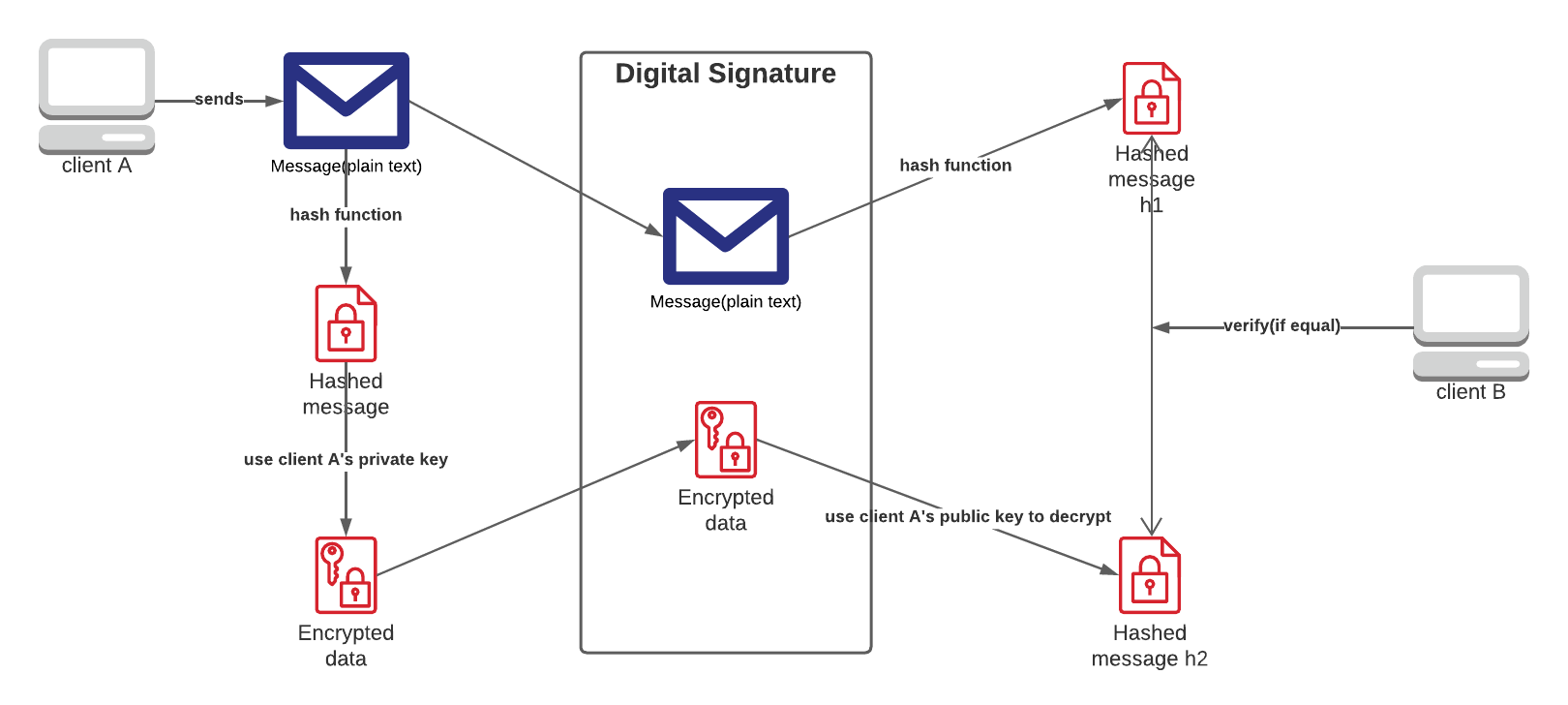
Generate digital signatures using RSA

Encrypting the hashed message using the private key:

s = m^d (mod n)

Decrypting the hashed message using the public key:

m = s^e (mod n)

Security

Attack capability: attacker knows signer’s public key pk

Chosen-message attacks(CMA)

• should be unforgeable even if the attacker can see many valid signatures on many messages, even messages chosen by the attacker.

Attack goal:

• Existential UnForgeability (EUF):
  • Should be infeasible for an attacker to produce any valid (msg, sig) pair where msg has not been signed by the honest signer (even for randomly looking msg)

Reference

Monash Uni FIT2093