Diffie-Hellman key exchange and EL Gamal PKE

Introduction

Diffie-hellman key exchange is a crypto that is widely used. You can see it everywhere:

• SSL/TLS: web
• IPsec: IPpackets
• Bluetooth
• 5G
• IOT

In this blog, we are looking into DHKE, to see how it works. Moreover, EL Gamal PKE is a crypto that is based on DHKE, we will learn this as well.

How DHKE works

Let’s say we have Alice and Bob will use their public keys to encrypt a message and private keys to decrypt a message.

Alice’s public key: A
Alice’s private key: a
Bob’s public key: B
Bob’s private key: b

public parameters: p and g, p is a prime number, g<p

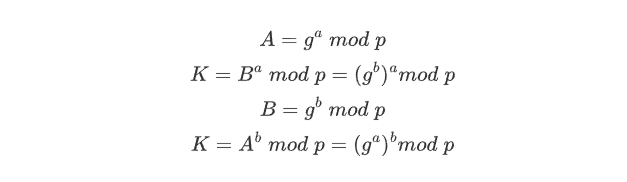
According to the formulas above, we can see that Alice and Bob will communicate the public keys and the shared keys they generate will be the same. Since there are some mathematical relationships between a private key and a public key, Alice or Bob can use their private keys and others’ public keys to get the shared key.

Then this shared key could be used in any symmetric cipher(like AES).

There’s a discrete log problem that prevents the shared key from being deduced by an attacker.

EL Gamal PKE

Differences

For PKE, both Alice and Bob will need to publish their public keys, while for EL-Gamal PKE, we only need one of them(receiver) to publish the public key.

For DHKE, it only explains how a shared key is generated, EL-Gamal PKE shows how a message could be encrypted and decrypted using DHKE.

A very strong and solid explanation here:

https://www.quora.com/What-is-the-difference-between-Diffie-Hellman-and-ElGamal

How it works

• Asymmetric crypto to generate a shared key

• symmetric crypto to encrypt a message

Scenario

Bob published his key to his website, and was happy with receiving messages from all.

Alice is sending a message to Bob.

Generate Public Key B(Bob)

• pick a random Prime(p), and a g such thatg<p
• pick a random private key b

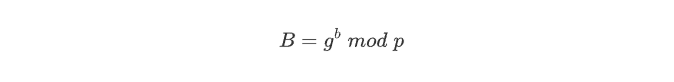
Bob’s public key set will be like <p,g,B>

Now Bob’s waiting for someone who is sending a encrypted message to him.

Encryption(Alice)

Alice picks a random private key a, then calculate the shared key K by using Bob’s public key B

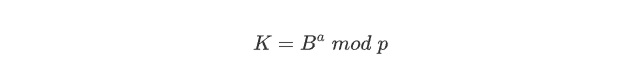
Generate public key A

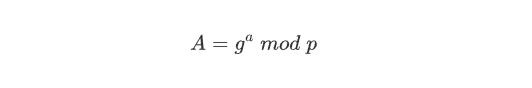
Then Alice uses the shared key K to encrypt a plaintext P to get a ciphertext C

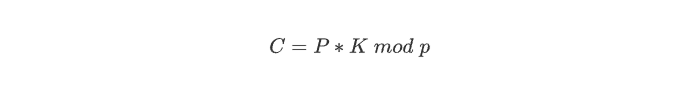
This actually used the symmetric crypto

Then Alice sends <A, C>(public key, ciphertext) to Bob

Decryption(Bob)

According to Alice’s public key A, Bob can calculate the shared key K

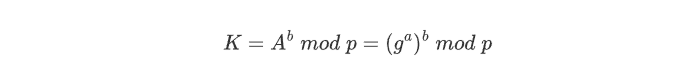
Then Bob decrypts the message by using the shared key K

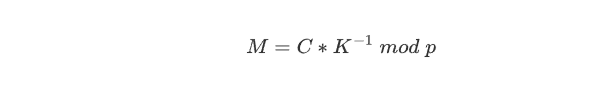
Calculation Trick

Square & Multiply Algorithm

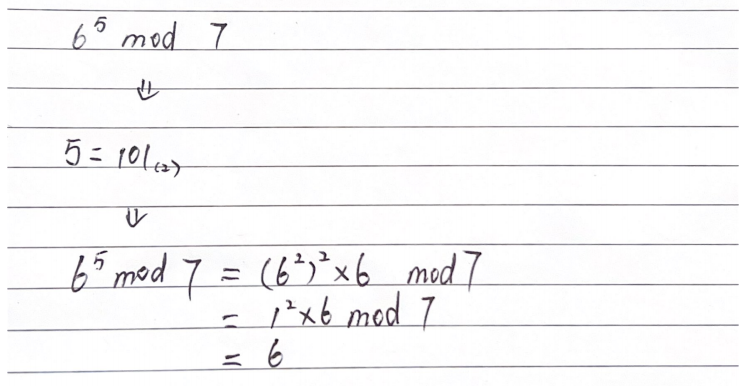
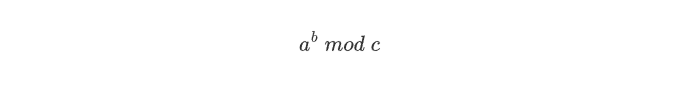
From the most left number(ignore it)

binary 0: square

binary 1: square then times a

RSA crypto

RSA key generation

choose two primes: p = 5 and q = 11

n = p*q = 5 * 11 = 55
ϕ(n)=(p-1)*(q-1)=4*10=40

Find two numbers e and e according to (e*d) mod ϕ(n) = 1, thus, e = 3, d = 27

Public key: (e,n)=(3, 55)

Private key: (d,n)=(27, 55)

RSA encryption

s = m^(e)mod n

RSA decryption

m = s^(d)mod n

Reference

Monash Uni FIT2093